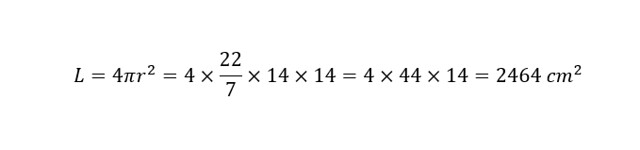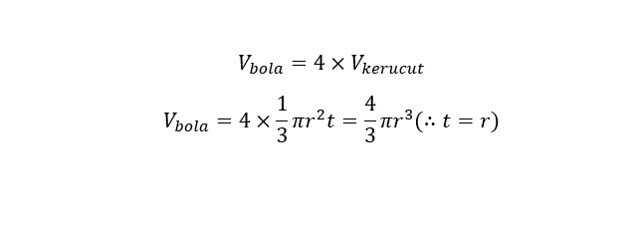LUAS PERMUKAAN BOLA

• Apakah kalian tahu perbedaan luas permukaan dan volume? Berbeda dengan bangun datar yang hanya memiliki luas, bangun ruang memiliki luas permukaan dan volume. Luas permukaan bangun ruang adalah jumlah luas seluruh permukaan bangun ruang. Sementara itu, volume adalah kapasitas ruang yang dapat ditempati pada bangun ruang. Kali ini, kita akan membahas cara menghitung luas permukaan dan volume bola.

Bola merupakan salah satu bangun ruang sisi lengkung. Apa itu? Bangun ruang sisi lengkung adalah kelompok bangun ruang yang memiliki bidang berbentuk lengkungan pada permukaannya. Selain bola, bangun ruang sisi lengkung lainnya adalah tabung dan kerucut.

Untuk mengukur luas permukaan dan volume bola, pertama-tama kita harus memahami bentuk bola terlebih dahulu. Bola adalah bangun ruang sisi lengkung yang terbentuk dari tak berhingga lingkaran yang berjari-jari sama dan berpusat di titik yang sama. Bola termasuk ke dalam bangun ruang sisi lengkung yang memiliki satu sisi.

Luas Permukaan Bola

Luas permukaan bola sama dengan empat kali luas lingkaran yang berjari-jari sama dengan jari-jari bola. Dalam matematika, kita dapat merumuskannya sebagai berikut.

Untuk memahaminya, yuk kita coba kerjakan contoh soal di bawah ini.

Tentukan luas permukaan bola dengan jari-jari 14 cm!

Karena jari-jari yang diketahui adalah 14 cm, kita hanya perlu memasukkannya ke dalam rumus.

Volume Bola

Kita bisa menemukan banyak benda berbentuk bola di sekitar kita, seperti bola sepak, buah semangka, dan kelereng. Menariknya, volume disini dapat diukur sebagai empat kali volume kerucut yang memiliki jari-jari alas dan tinggi yang sama dengan jari-jari bola. Karena itu, kita dapat mengukurnya dengan rumus berikut.

Supaya kita lebih paham, ayo kita kerjakan contoh soal di bawah ini.

Sebuah bola memiliki jari-jari 5,6 cm. Tentukan volume bola tersebut!

LUAS SELIMUT TABUNG

Rumus luas selimut tabung merupakan salah satu rumus mengenai bangun ruang atau geometri yang harus dipahami. Rumus pada mata pelajaran matematika ini sangat mudah untuk dipelajari.

Rumus luas selimut tabung juga sering ditemukan pada soal matematika di berbagai jenjang pendidikan, yaitu SD hingga perguruan tinggi.

Selain itu, mencari rumus luas selimut tabung ini juga bisa diterapkan dalam kehidupan sehari-hari.

Sebelum menghitung luas selimut dan melakukan perhitungan, maka kamu harus mengetahui bentuk tabung terlebih dahulu.

Dikutip dari Kamus Besar Bahasa Indonesia, kata tabung juga dapat diartikan sebagai silinder atau ruang yang berbatas bidang lengkung dan dua bulatan yang sama besar.

Hal itu menjadi keunikan tabung dibanding bangun ruang lainnya. Tabung memiliki alas dan tutup bangun ruang berbentuk bulatan atau lingkaran.

Tabung ini berbeda dengan kerucut meskipun sama-sama memiliki alas berbentuk lingkaran. Perbedaannya, kerucut tidak memiliki tutup lingkaran, tetapi bentuk tutupnya mengerucut.

Tabung memiliki alas dan tutup berbentuk lingkaran. Sementara itu, selimut tabung berbentuk persegi empat. Jadi, rumus luas selimut tabung adalah:

Rumus luas selimut tabung = Keliling lingkaran x Tinggi tabung

Rumus mencari luas selimut tabung terdiri dari dua bagian, yaitu “keliling lingkaran” dan “2 x phi x jari-jari”.

Hasil keliling lingkaran tabung ini digunakan sebagai panjang atau lebar yang digunakan untuk mencari luas persegi empat.

Keliling lingkaran alas tabung ini kemudian dikalikan dengan tinggi tabung untuk mendapatkan luas selimut tabung. 

Salah satu hal paling penting untuk memahami matematika adalah menambah banyak frekuensi latihan soal agar dapat menggunakan rumus ini.

Coba kerjakan contoh soal luas selimut tabung berikut ini agar kamu dapat lebih memahami dan mampu mengaplikasikan rumus dari luas selimut tabung.

Contoh Soal

Ganesha diberikan celengan oleh kakeknya. Celengan itu terbuat dari kaleng bekas makanan ringan. Celengan Ganesha berbentuk tabung dengan jari-jari 7 cm dan tinggi 20 cm.

Supaya lebih indah, Ganesha ingin menutup celengan tersebut dengan bungkus kado. Hanya bagian selain alas dan tutup tabung yang ingin Ganesha tutup.

Berapa luas bungkus kado yang dibutuhkan Ganesha untuk menutup selimut tabung?

Penyelesaian:

Apakah kamu berhasil mengerjakan soal di atas? 

Mari kita bahas pengerjaan soal matematika ini bersama-sama.

Seperti yang dijelaskan sebelumnya, rumus untuk mencari luas selimut tabung dapat dihitung setelah menghitung keliling tutup atau alas lingkaran tabung tersebut.

Melalui rumus “2 x phi x jari-jari”, maka keliling lingkaran tersebut dapat kamu cari dengan perhitungan “2 x 22/7 x 7 cm”. Hasil perhitungan ini adalah 44 cm.

Selanjutnya, rumus volume dan luas selimut tabung dapat kamu operasikan dengan mengalikan keliling lingkaran tersebut dan tinggi tabung.

Rumus luas selimut tabung dioperasikan dengan perhitungan “44 cm x 20 cm”. Hasil perkalian ini adalah 880 cm persegi.

Jadi, luas selimut tabung celengan Ganesha adalah 880 cm persegi.

Itulah penjelasan lengkap mengenai rumus luas selimut tabung disertai contoh dan pembahasan soalnya. Perbanyak berlatih rumus agar kamu bisa menghadapi ujian dengan baik.

Luas Permukaan Tabung Beserta Contoh Soalnya

Berikut tips dan trik menghitung luas permukaan tabung beserta contoh soal beserta jawabannya.

27/1/2022, 19.39 WIB 

Tabung atau silinder merupakan bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Struktur bentuk, tabung memiliki tiga sisi dan dua rusuk. 

Dalam kehidupan sehari-hari, tabung digunakan dalam berbagai macam manfaat. Hal itu sering ditemukan di dapur dan terowongan jalan hingga tabung gas yang sering digunakan masak. Oleh karenanya dalam pembahasan ini akan dijelaskan mengenai luas permukaan tabung. 

Permukaan tabung terdiri dari semua titik pada baris yang sejajar dengan garis yang diketahui dan melewati tetap kurva pesawat yang tidak sejajar dengan garis yang diberikan. Pada garis tersebut kelompok garis sejajar atau disebut juga elemen permukaan tabung. 

Permukaan Tabung adalah permukaan yang dilacak oleh sebuah garis yang disebut generatrix yang sejajar dengan dirinya sendiri dan selalu melewati budang directrix yang tidak sejajar. Posisi tertentu dari matrik generatrik adalah elemen permukaan tabung. 

Untuk menghitung luas permukaan tabung dimulai dari jari-jari (r). Jaring-jaring tabung terdiri dari tutup dan alas tabung yang berbentuk lingkaran, sehingga rumus luas dari alas dan tutup yang berbentuk lingkaran yaitu = 2π r². Untuk nilai phi (π) dapat menggunakan 22/7 atau 3,14. Hal itu dapat dilihat dari bagian melengkung yang mengelilingi tabung, memiliki bentuk persegi panjang mempunyai rumus luas panjang x lebar. Panjangnya sama dengan keliling lingkaran sedangkan lebarnya sama dengan tinggi tabung, sehingga rumus luas sisi lengkungnya adalah 2π r t. 

Rumus luas jaring-jaring tabung : Rumus luas alas dan tutup : π.r2 Rumus luas selimut : 2.π.r.t Dari kedua rumus ini, kita akan bisa menuliskan rumus luas permukaan tabung menjadi: Luas permukaan tabung = 2 x Luas alas + Luas selimut tabung Luas permukaan tabung = 2 x (π x r2) + 2 x π x r x t = 2 x π x r x ( r + t ) 

Untuk bisa lebih memahami hal ini, mari kita lihat salah satu contoh soal berikut ini: 

1. Soal Pertama Untuk membuat sebuah patung, pengrajin menggunakan sebuah batang pohon yang berbentuk seperti tabung dengan diameter 14 cm dan tinggi 18 cm. 

Tentukan luas permukaan dari batang kayu tersebut. 

Penyelesaian: Dari soal di atas kita mendapatkan informasi seperti: d = 14 cm, maka jari-jarinya adalah r = 7 cm t = 18 cm Dengan begitu kita tinggal memasukannya kedalam rumus. Jawab: Lp = 2 x π x r x ( r + t ) = 2 x 22/7 x 7 (7 + 18 ) = 44 x 25 = 1.100 cm2 

2. Soal Kedua Berapa volume tabung jika memiliki diameter 50 cm dan tinggi 66 cm? Diketahui: Diameter = 50 cm, karena r = 1/2 diameter maka r = 25 cm tinggi = 66 cm Rumus: Volume Tabung = π x r² x t Jawaban: π x r² x t = (22/7) x 25cm² x 66 cm = (22/7) x 25 x 25 x 66 = (22/7) x 41250 = 129.642 cm³ 

Demikianlah rumus permukaan tabung.

About us:

MESMERIC: SURABAYA BLACK METAL

SSB PURWODADI GROBOGAN

DESAIN BESAR OLAH RAGA NASIONAL (DBON)

*Assalammualaikum wr wb,

Selamat Siang... Salam Sejahtera..*

Menindaklanjuti Peraturan Presiden Republik Indonesia (Perpres) Nomor 86 Tahun 2021 tentang Desain Besar Olahraga Nasional (DBON) dengan visi Mewujudkan Indonesia Bugar, Berkarakter Unggul, dan Berprestasi Dunia, maka Kementerian Pendidikan, Kebudayaan, Riset dan Teknologi, melalui Direktorat Jenderal Guru dan Tenaga Kependidikan, Direktorat Guru Pendidikan Menengah dan Pendidikan Khusus akan mengumpulkan data melalui survei dalam rangka Penyiapan Bahan dan Pemetaan Program Transformasi Guru Pendidikan Jasmani, Olahraga, dan Kesehatan (PJOK) yang hasilnya akan digunakan untuk memberikan input/rekomendasi dalam transformasi kinerja guru dan talenta PJOK. 

*Kami harapkan kesediaan Bapak/Ibu Kepala Dinas Pendidikan untuk mendukung kegiatan survei ini* dengan cara menyebarluaskan laman survei ini untuk dapat diisi oleh *Guru PJOK* di Seluruh Indonesia, pada link : 

https://bit.ly/surveiprofilgurupjok

atas bantuan dan perhatiannya kami sampaikan Terimakasih.

🙏

About Us:

GROBOGAN BLACK METAL

youtube

JADWAL PELAJARAN TK/PAUD

JADWAL PELAJARAN TK DHARMA WANITA I KEDUNGREJO NO WAKTU SENIN SELASA RABU KAMIS JUM’AT SABTU Keg. Awal Keg. Awal Keg. Awal Keg. Awal Keg. Awal Keg. Awal 1 07.00-08.00 MASEK BAHASA SENI MASEK MASEK FISIK MRK 2 Keg. Inti Keg. Inti Keg. Inti Keg. Inti Keg. Inti Keg. Inti 3 08.00-09.00 BAHASA KOGNITIF BAHASA KOGNITIF BAHASA KOGNITIF 4 KOGNITIF FISIK MRK KOGNITIF FISIK MRK KOGNITIF MASEK 5 FISIK MRK SENI FISIK MRK BAHASA FISIK MRK SENI 6 09.00-09.30 Istirahat Istirahat Istirahat Istirahat Istirahat Istirahat 7 Keg Akhir Keg Akhir Keg Akhir Keg Akhir Keg Akhir Keg Akhir 8 09.30-10.00 SENI MASEK MASEK SENI SENI BAHASA Kedungrejo, Kepala TK Dharma Wanita I Kedungrejo SRI WIDIANINGSIH, S.Pd. NIP.